Rumus
yang digunakan pada aturan cramer ini dijamin pada Teorema, dimana bunyi
teoremanya adalah sebagai berikut :
Teorema :
Jika Ax = B adalah
sistem yang terdiri dari n persamaan linier dalam n bilangan tak diketahui
sehingga det(A) ≠ 0, maka sistem tersebut mempunyai yang unik, dimana pemecahan
ini yakni sebagai berikut
Keterangan :
Dimana
Aj adalah matriks yang kita dapatkan dengan menggantikan entri-entri dalam
kolom ke-j dari A dengan entri-entri dalam matriks
Tambahan :
· Matriks A1 dibentuk
dari matriks A dengan mengganti entri-entri kolom pertamana pada matriks A dengan
nilai-nilai pada sebelah kanan sama dengan (=) dari persamaan.
· Matriks A2 juga
dibentuk dengan cara mengganti entri-entri kolom kedua.
·
Begitu juga untuk
membentuk matriks An yaitu dengan mengganti entri-entri pada kolom n.
Soal-soal persamaan
linier dengan aturan cramer
1.
Gunakanlah aturan
Cramer untuk memecahkan Permasalahan persamaan linier dan cari nilai x,y,z
dengan aturan cramer
x
+ 3y + 5z = 3
x
+ y + 2z = 6
9x
+ 5y + 6z = 9
Jawab
:
>>A=[2
3 5;7 1 2;9 5 6]
A
=
2
3 5
7
1 2
9
5 6
>>
B=[3;6;9]
B
=
3
6
9
>>
A1=[3 3 5;6 1 2;9 5 6]
A1
=
3
3 5
6
1 2
9
5 6
>>
A2=[2 3 5;7 6 2;9 9 6]
A2
=
2
3 5
7
6 2
9
9 6
>>
A3=[2 3 3;7 1 6;9 5 9]
A3
=
2
3 3
7
1 6
9
5 9
>>
X=det(A1)/det(A)
X
=
0.7800
>>
Y=det(A2)/det(A)
Y
=
0.1800
>>
Z=det(A3)/det(A)
Z
=
0.1800
2. Gunakanlah aturan Cramer untuk memecahkan
2. Gunakanlah aturan Cramer untuk memecahkan
Jawab
:
>>
A=[1 0 2;-3 4 6;-1 -2 3]
A
=
1
0 2
-3
4 6
-1
-2 3
>>
A1=[6 0 2;30 4 6;8 -2 3]
A1
=
6
0 2
30
4 6
8
-2 3
>>
A2=[1 6 2;-3 30 6;-1 8 3]
A2
=
1
6 2
-3
30 6
-1
8 3
>>
A3=[1 0 6;-3 4 30;-1 -2 8]
A3
=
1
0 6
-3
4 30
-1
-2 8
>>
X1=det(A1)/det(A)
X1
=
-0.9091
>>
X2=det(A2)/det(A)
X2
=
1.6364
>>
X3=det(A3)/det(A)
X3
=
3.4545
Untuk lebih memahami lebih lanjut mengenai materi matematika komputasi, bisa mengunjungi

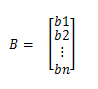





Tidak ada komentar:
Posting Komentar