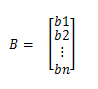TUGAS 5 (CARA MENGHITUNG HARGA TOTAL SUATU BARANG DENGAN MENGGUNAKAN MATLAB)

CARA MENGHITUNG HARGA TOTAL SUATU BARANG DENGAN MENGGUNAKAN MATLAB

Langkah-Langkahnya sebagai berikut :

a=input('Gula = ');

b=input('Permen = ');

c=input('Nugget = ');

d=input('Sabun = ');

e=input('Coklat = ');

Jh=a+b+c+d+e;

Td=10/100*(a+b+c+d+e);

Tb=Jh-Td;

disp(['Jumlah Harga = ' num2str(Jh)]);

disp(['Total Harga Diskon = ' num2str(Td)]);

disp(['Total Bayar = ' num2str(Tb)])

>> Totalbarang

Gula = 10000

Permen = 5000

Nugget = 21000

Sabun = 3000

Coklat = 21000

Jumlah Harga = 60000

Total Harga Diskon = 6000

Total Bayar = 54000

gambar 2c

Untuk lebih memahami lebih lanjut mengenai materi matematika komputasi, bisa mengunjungi

http://jefrimarzal.staff.unja.ac.id/category/pengajaran/mtkkomputasi

TUGAS 4 (GRAFIK 3D DENGAN MENGGUNAKAN MATLAB)

GRAFIK 3D DENGAN MENGGUNAKAN MATLAB

>> vx=[-4:0.2:4];

>> vy=[-3:0.2:3];

>> [x,y]=meshgrid(vx,vy);

>> z=x.*y.*(x.^2-y.^2)./(x.^2+y.^2+eps);

>> figure

>> plot3(x,y,z)

>> grid on

>> figure

>> mesh(x,y,z)

>> view(-37,15)

Gambar 1a

>> mesh(x,y,z)

>> view(-28,19)

>> surfc(x,y,z)

Gambar 1b

>> colormap hot

Gambar 1c

>> shading interp

>> colormap hsv

Gambar 1d

>> x=[-4:0.5:4];

>> [x,y]=meshgrid(x,x);

>> z=1./(3+x.^2+y.^2);

>> surfl(z)

>> shading interp

>> colormap hot

>> xlabel('x');

>> ylabel('y');

Gambar 1

>> z=peaks(25);

>> figure

>> mesh(z)

gambar 2a

>> z=peaks(25);

>> figure

>> mesh(z)

>> surf(z)

>> colormap(jet)%change color map

gambar 2b

>> z=peaks(25);

>> figure

>> mesh(z)

>> surf(z)

>> colormap(jet)%change color map

>> surfl(z)

>> colormap(pink)%change color map

>> shading interp %interpolate colors ac

gambar 2c

Untuk lebih memahami lebih lanjut mengenai materi matematika komputasi, bisa mengunjungi

http://jefrimarzal.staff.unja.ac.id/category/pengajaran/mtkkomputasi

TUGAS 3 (4 FUNGSI POLINOMIAL)

4 fungsi Polinomial

Penyelesaian :

>> x=[-10:0.5:10];

>> y1=x.^4-12*x.^3+25*x+116;

>> y2=x.^4-25*x.^3+12*x.^2+36*x+40;

>> y3=x.^4+9*x.^3+70*x.^2+17*x-20;

>> y4=x.^4-15*x.^3-35*x.^2-20*x+13;

>> plot(x,y1);

>> hold on

>> plot(x,y2);

>> hold on

>> plot(x,y3);

>> hold on

>> plot(x,y4);

>> hold on

>> plot(x,y1,'r')

>> plot(x,y2,'g')

>> plot(x,y3,'m')

>> plot(x,y4,'b')

>> grid on

>> plot(x,y1,'*r')

>> plot(x,y2,'*g')

>> plot(x,y3,'*m')

>> plot(x,y4,'*b')

>> plot(x,y1,'*r')

>> plot(x,y2,'*g')

>> plot(x,y3,'*m')

>> plot(x,y4,'*b')

gambar 2c

Untuk lebih memahami lebih lanjut mengenai materi matematika komputasi, bisa mengunjungi

http://jefrimarzal.staff.unja.ac.id/category/pengajaran/mtkkomputasi

TUGAS 2 (Penyelesaian Soal Persamaan Linier dengan Aturan Cramer)

Rumus yang digunakan pada aturan cramer ini dijamin pada Teorema, dimana bunyi teoremanya adalah sebagai berikut :

Teorema :

Jika Ax = B adalah sistem yang terdiri dari n persamaan linier dalam n bilangan tak diketahui sehingga det(A) ≠ 0, maka sistem tersebut mempunyai yang unik, dimana pemecahan ini yakni sebagai berikut

Keterangan :

Dimana Aj adalah matriks yang kita dapatkan dengan menggantikan entri-entri dalam kolom ke-j dari A dengan entri-entri dalam matriks

Tambahan :

·          Matriks A1 dibentuk dari matriks A dengan mengganti entri-entri kolom pertamana pada matriks A dengan nilai-nilai pada sebelah kanan sama dengan (=) dari persamaan.

·          Matriks A2 juga dibentuk dengan cara mengganti entri-entri kolom kedua. 

·           Begitu juga untuk membentuk matriks An yaitu dengan mengganti entri-entri pada kolom n.

Soal-soal persamaan linier dengan aturan cramer

1.      Gunakanlah aturan Cramer untuk memecahkan Permasalahan persamaan linier dan cari nilai x,y,z dengan aturan cramer

x + 3y + 5z = 3

x + y + 2z   = 6

9x + 5y + 6z = 9

Jawab :

        >>A=[2 3 5;7 1 2;9 5 6]

        A =

            2     3     5

            7     1     2

            9     5     6

  

        >> B=[3;6;9]

        B =

            3

            6

            9 

  

        >> A1=[3 3 5;6 1 2;9 5 6]

        A1 =

              3     3     5

              6     1     2

              9     5     6

        >> A2=[2 3 5;7 6 2;9 9 6]

         A2 =

              2     3     5

              7     6     2

              9     9     6

       >> A3=[2 3 3;7 1 6;9 5 9]

       A3 =

             2     3     3

             7     1     6

             9     5     9

       >> X=det(A1)/det(A)

        X =

            0.7800

      >> Y=det(A2)/det(A)

       Y =

          0.1800

       >> Z=det(A3)/det(A)

        Z =

            0.1800
2. Gunakanlah aturan Cramer untuk memecahkan

      

          Jawab :

          >> A=[1 0 2;-3 4 6;-1 -2 3]

         A =

               1     0     2

              -3     4     6

              -1    -2     3

        >> A1=[6 0 2;30 4 6;8 -2 3]

        A1 =

               6     0     2

             30     4     6

               8    -2     3

  

       >> A2=[1 6 2;-3 30 6;-1 8 3]

  

       A2 =

             1     6     2

            -3    30     6

            -1     8     3

      >> A3=[1 0 6;-3 4 30;-1 -2 8]

      A3 =

           1     0     6

          -3     4    30

          -1    -2     8 

      >> X1=det(A1)/det(A)

      X1 =

           -0.9091

     >> X2=det(A2)/det(A)

     X2 =

           1.6364

  

     >> X3=det(A3)/det(A)

      X3 =

           3.4545

Untuk lebih memahami lebih lanjut mengenai materi matematika komputasi, bisa mengunjungi

http://jefrimarzal.staff.unja.ac.id/category/pengajaran/mtkkomputasi

TUGAS 1 (PEMBAGIAN MATRIKS (ARRAY DIVISION))

PEMBAGIAN MATRIKS (ARRAY DIVISION)

Pembagian matriks pada MATLAB menggunakan fundamental dari aljabar linier. Sebelum ke Array division perlu diketahui tentang :

·         Matriks identitas

Matriks identitas adalah matriks persegi yang diagonal utamanya adalah 1 dan elemen lainnya adalah 0. Dalam konsep lajabar linier setiap matriks identitas hasilnya matriks itu sendiri.

·         Matriks invers

Invers matriks A dapat didefinisikan sebagai matriks bujursangkar B sedemikian hingga matriks A dioperasikan A B = B A = I, dimana I matriks identitas. Sedemikian B disimbolkan dengan A^-1

Untuk mencari invers suatu matriks dapat menggunakan syntax inv(variabel) menggunakan MATLAB. Misalkan mencari invers matriks A yang didefinisikan sebagai berikut:

   ·       Determinan matriks

Determinan matriks adalah fungsi khusus yang mengasosiasikan suatu bilangan real dengan suatu matriks bujursangkar. Determinan matriks MATLAB menggunakan fundamental aljabar linier sebgai konsep dasarnya. Untuk menghitung determinan suatu matriks berukuran m x n dapat menggunakan syntax det(variabel). Misalkan akan menghitung determinan matriks E yang berukuran 5 x 5.

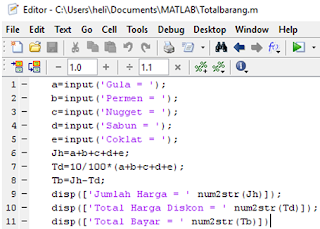
Script advenesia

MATLAB mempunyai 2 jenis pembagian yaitu right division(/) dan left division(\)

a.      Right Division

Misalkan matriks A dibagi dengan matriks B menghasilkan matriks C dapat diformulasikan sebagai berikut :

C = AB^-1

C = A/B

Misalkan diketahui :

           Sehingga nilai C dapat dihitung dengan syntax berikut :

           Script advernesia

b.      Left division

Misalkan matriks D dibagi dengan matriks E menghasilkan matriks F dapat diformulasikan sebagai berikut :

F = D^-1E

F = D\E

Misalkan diketahui 

Untuk lebih memahami lebih lanjut mengenai materi matematika komputasi, bisa mengunjungi
http://jefrimarzal.staff.unja.ac.id/category/pengajaran/mtkkomputasi